Hey,
A little technical update today. We have been playing with Bayes optimal allocation in the case of a 2-arm Bernoulli Bandit problem with finite (and rather small) horizon. The idea is to start comparing some currently popular solutions (e.g., Thompson sampling, Gittins Index, etc.) to Bayes optimal allocation (yes, some of this has been done before…).
So, we started out implementing induction the algorithm described here in [R]. You can find the source file here. The use is straightforward:
source("bb.R")
# Arm priors:
arm1 <- c(1,1)
arm2 <- c(120,100)
# Number of remaining pulls:
n <- 5
# Compute the Delta between the arms:
res <- DeltaArm(n, arm1, arm2)
# Print result, and which arm to play
print(res)
print(ifelse(res>0,"Arm1","Arm2"))
Which prints that Arm 1 should be preferred in this case (note that this is not the case when $n < 3$; for these values the exploration does not pay off since there are too little future opportunities to use the learned knowledge).
However, the implementation in bb.R ends up being a bit slow, so, using the Rcpp package, we implemented the same thing in C++. This can be called like this:
# Use the Cpp version
library(Rcpp)
# Load the compiled Cpp function:
dyn.load('BB.so')
# Arm priors:
arm1 <- c(1,1)
arm2 <- c(120,100)
# Number of remaining pulls:
n <- 5
# Compute the Delta between the arms:
res <- .Call('DeltaArm', arm1[1],arm1[2],arm2[1],arm2[2],n)
# Print result, and which arm to play
print(res)
print(ifelse(res>0,"Arm1","Arm2"))
Which gives the exact same (well, with some different rounding) results but much faster.
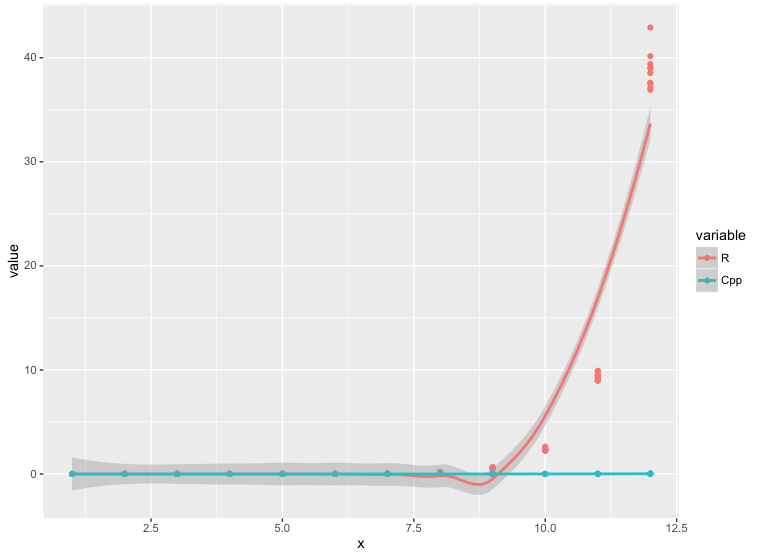
How much faster is easily seen if when doing several runs ($m=10$ in this case), for different values of the horizon $n = 1, \dots, 12$. The figure below shows the time progression of the R version and the C++ version; quite a shocking difference really. The C++ version can be downloaded in our downloads section (both the source, as well as the compiled version).
Have a great weekend!